Par Paul Calberg-Ellen*

Dans le cadre de projets de construction ou de rénovation énergétique de bâtiments, les maîtres d’ouvrage font appel à un certain nombre d’outils et de méthodes qui permettent de contrôler les consommations énergétiques après travaux afin d’en évaluer la performance.

Parmi ces outils, les contrats avec Garantie de Résultats Énergétiques (GRE) permettent d’une part d’assurer financièrement d’une part le maître d’ouvrage par le fournisseur de service (entreprise qui réalise les travaux) dans le cas où les objectifs contractuels de performance énergétique n’ont pas été atteints/respectés et d’autre part le fournisseur de service par la maîtrise d’ouvrage dans le cas où la consommation d’énergie aurait dépassé les objectifs contractuels.

Introduction

Dans le cadre d’un contrat avec garantie de résultats énergétiques, l’un des points cruciaux est la comparaison entre la valeur mesurée après travaux et la valeur de l’engagement sur laquelle a été fixé le contrat, en général déterminée par l’intermédiaire d’une simulation énergétique (via un logiciel de SED ou STD). Ces valeurs sont associées à des incertitudes (pour plus d’information, voir IPMVP : « Principes fondamentaux – protocole international de mesure et de vérification de la performance »).

Il est possible de faire une analogie entre ce qui se passe dans le cadre d’un contrat avec garantie de résultats énergétique, et ce qui se passe dans le cadre d’un processus de production industriel.

Dans un processus de production industriel, client et producteur définissent des spécifications sur les produits. Lorsque celles-ci sont des grandeurs physiques (dimensions, masse, etc.), il est souvent utile de maîtriser les problèmes liés à la précision finie du processus (fabrication des pièces, contrôle de production, etc.).

Les documents JCGM 106 :2012 et FD X07-022 font ainsi référence à l’évaluation de la conformité de produits, en mettant entre autres en avant les notions de « risque producteur » et de « risque client ». Celles-ci permettent aux clients et producteurs de prévoir les risques de non-conformité du processus d’ensemble (depuis la fabrication jusqu’à la réception par le client) en fonction des caractéristiques du processus (incertitude de mesure, etc.).

En développant l’analogie entre les deux processus, l’article « Évaluation du coût du risque pour le maître d’ouvrage et le fournisseur de services dans le cadre d’un contrat à garantie de résultats énergétiques » propose d’estimer le coût des risques dans le cadre d’une GRE pour chacune des parties en fonction des différents paramètres identifiés : incertitude sur la mesure, incertitude sur la simulation, position de l’engagement, largeur de l’intervalle de tolérance (ou tunnel de neutralisation).

Nous présentons ici quelques éléments issus de cet article. Précisons tout d’abord plus en détail le contexte.

Mise en contexte

Dans le contexte d’un contrat avec GRE on définit les contractants de la manière suivante :

• le fournisseur de service est le contractant qui s’engage à faire baisser la consommation énergétique du bâtiment considéré;
• le maître d’ouvrage est le contractant qui souhaite faire baisser la facture énergétique de son bâtiment et qui s’est adressé au fournisseur de service.

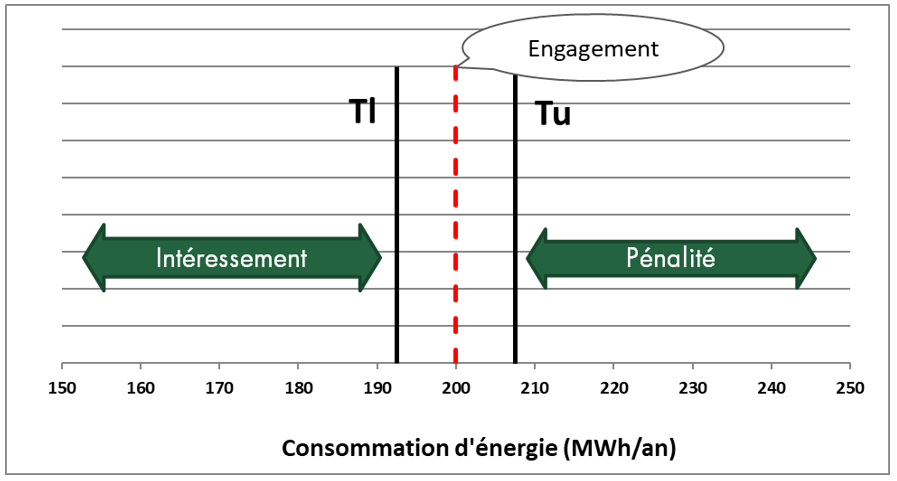
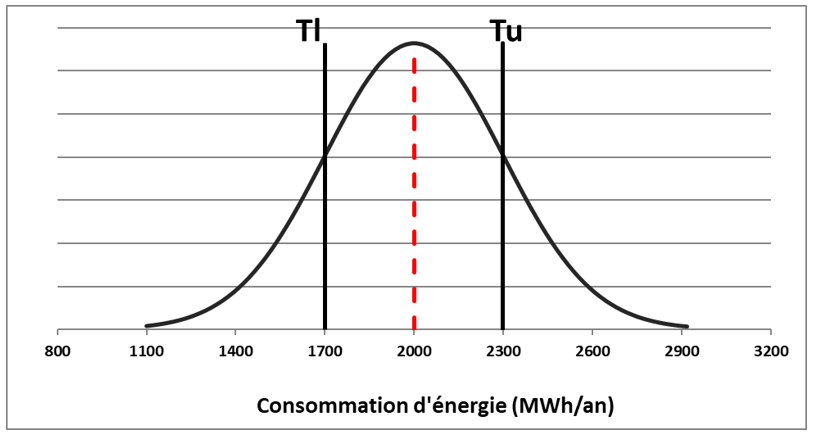
Les contractants définissent un seuil : « l’engagement » autour duquel ils s’accordent sur un intervalle de tolérance (appelé classiquement « tunnel de neutralité »). Si la valeur mesurée est supérieure à la borne supérieure (Tu) de l’intervalle de tolérance, alors le fournisseur de service paie une pénalité. En parallèle, si la valeur est inférieure à la borne inférieure (Tl) le fournisseur de service touchera un intéressement.

Graphique 1

Illustration de l’engagement, des bornes de l’intervalle de tolérance, et des zones de pénalité et d’intéressement

 

Si η_m  < Tl :

Intéressement = p * (Tl - η_m)

 

Si η_m > Tu :

Pénalité = p * (η_m - Tu)

Avec p [€.kWh^-1] le coût unitaire de l’énergie.

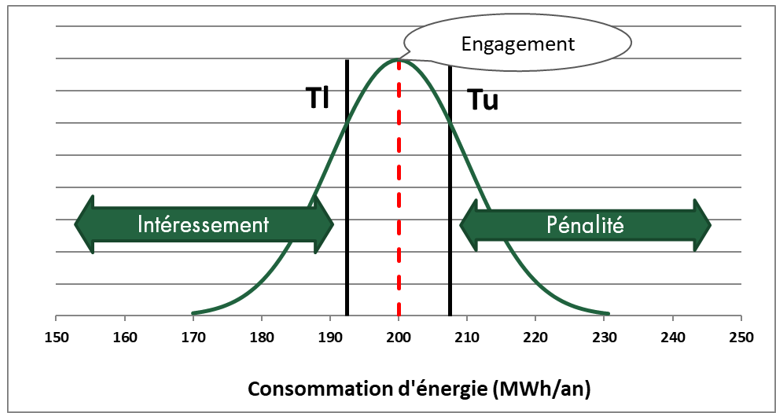
On considère ici que le fournisseur de service a déterminé son engagement en utilisant une simulation énergétique dynamique (SED), qui lui a fourni une prédiction de consommation, et l’incertitude associée à l’engagement. Le calcul de l’incertitude est aujourd’hui possible grâce à certains logiciels de simulation énergétique dynamique, qui implémentent des algorithmes de propagation d’incertitude. On peut alors positionner l’engagement et l’intervalle de tolérance (tunnel de neutralité) par rapport à l’incertitude associée à la simulation, représentée sous la forme d’une densité de probabilité.

 Graphique 2

Illustration de la densité de probabilité représentant l’incertitude de simulation, par rapport à l’engagement et à l’intervalle de tolérance

La mesure réalisée pour définir la valeur η_m  est entachée d’une incertitude. La valeur mesurée peut dès lors se trouver hors de l’intervalle de tolérance alors que la valeur réelle appartenait à cet intervalle, ou inversement. On peut ainsi distinguer deux types de risques :

• le gain manqué : l’une des parties prenantes aurait dû « gagner » plus que ce qu’elle n’a gagné;
• le risque d’avoir trop payé : l’une des parties prenantes a payé plus que ce qu’elle aurait effectivement dû payer.

 

Graphique 3

Illustration de l’incertitude de mesure, par rapport à l’intervalle de tolérance sur l’engagement.

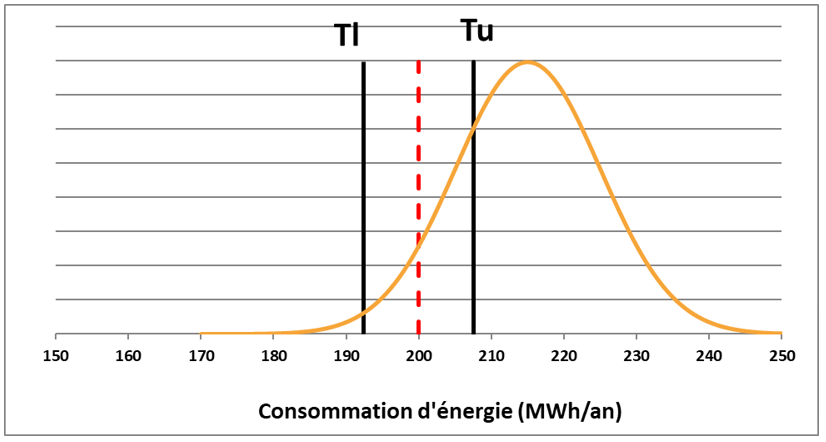
Note de lecture : pour une valeur vraie de la mesure valant 215 MWh (sommet de la courbe jaune), soit au-dessus de Tu, borne supérieure de l’intervalle de tolérance, il est possible, à cause de l’incertitude de mesure, d’obtenir une lecture de la mesure qui se situerait à l’intérieur de l’intervalle de tolérance (cela se traduit par le fait que la courbe jaune, qui matérialise la densité de probabilité de la mesure, n’est pas nulle à cet endroit)

Exemples de risque

Comme vu précédemment, le maître d’ouvrage sera amené :

Si η_m  < Tl : à verser l'intéressement au fournisseur de service.

Si η_m > Tu : à toucher les pénalités.

 Graphique 4

Risques maître d'ouvrage

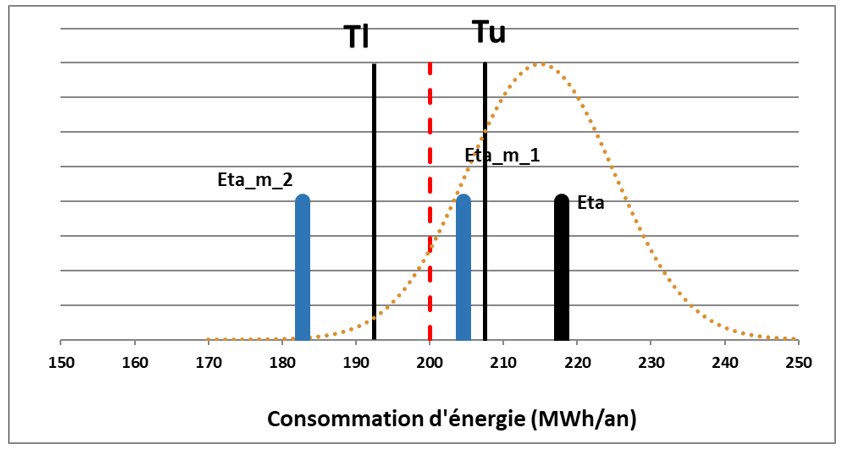
Sur le graphique précédent, deux cas sont présentés (pour illustration - l’ensemble des cas possibles n’est pas détaillé ici) :

(1) Tl < η_m1 < Tu  et Tu < η

Dans le cas (1), le maître d’ouvrage n’a rien perçu alors qu’il aurait dû percevoir quelque chose, c’est un gain manqué.

(2) η_m2 < Tl  et  Tu < η

Dans le cas (2), le maître d’ouvrage a payé un intéressement alors qu’il aurait dû percevoir des pénalités, c’est un gain manqué et un trop payé.

Pour les risques encourus par le fournisseur de service, la logique est inversée par rapport au maître d’ouvrage. Le fournisseur de service sera amené :

- si η_m < Tl, à percevoir l'intéressement

- si η_m > Tu, à payer des pénalités

Application sur un cas concret

Intervalle de tolérance centré autour de la valeur du mesurande

Une entreprise modélise la consommation énergétique d’un bâtiment après travaux. Le résultat de la simulation est une consommation annuelle de 2 000 MWh/an (tous postes confondus, pour une surface de 10 000 m²), associée à une incertitude-type de u₀ = 15 % de y₀.

Un contrat de performance énergétique est établi entre le maître d’ouvrage et l’entreprise. La limite de déclenchement de l’intéressement est 1 700 MWh (Tl) et celle de déclenchement des pénalités est 2 300 MWh (Tu), soit un intervalle de tolérance de +/- 15 % de y₀. Le montant de l’intéressement et des pénalités est proportionnel à l’écart entre la mesure et la limite et est de 0,1 € par kWh de différence.

Graphique 5

Illustration de la densité de probabilité de la prévision de consommation pour l’exemple avec intervalle centré

 

On peut alors calculer, grâce aux équations proposées dans l’article « Évaluation du coût du risque pour le maître d’ouvrage et le fournisseur de services dans le cadre d’un contrat à garantie de résultats énergétiques », que le coût du risque total est le suivant, en fonction de l’incertitude-type de mesure :

Tableau 1

Coût du risque pour u₀ = 15% y₀

On constate ainsi que la réduction de l’incertitude-type de mesure de 15 % à 5 % permet de réduire le risque d’environ 3 800 €/an (pour une incertitude-type de simulation de 15 % de y₀ et un intervalle de tolérance de +/- 15 % de y₀.). Si l’engagement est prévu sur une durée de 10 ans, il sera donc intéressant d’un point de vue économique d’investir dans une amélioration du système de mesure faisant passer l’incertitude-type de mesure de 15 à 5 % pour un coût inférieur à 38 000 €.

Dans ce cas de figure, on peut également montrer que :

→  le coût du risque total est également réparti entre le maître d’ouvrage et le fournisseur de service;

→  les deux parties ont intérêt à réduire l’incertitude-type de mesure et l’incertitude de simulation, afin de diminuer le coût du risque.

Intervalle « décentré » autour d’une valeur d’engagement surestimée

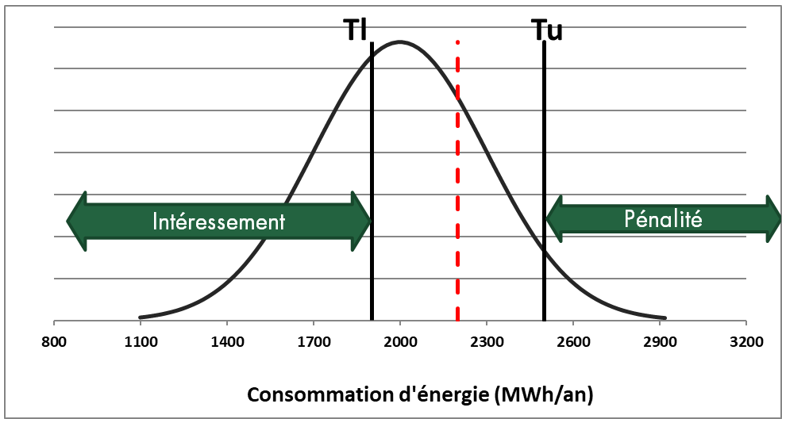
Ici on utilise les mêmes caractéristiques que pour le problème précédent, mais l’intervalle de tolérance est « décentré » autour d’une valeur moyenne d’engagement y₀’ (moyenne de Tl et Tu) surestimée qui correspond à 110 % de la valeur y₀.

Graphique 6

Illustration de la densité de probabilité représentant l’incertitude de simulation, par rapport à l’engagement et à l’intervalle de tolérance, dans le cas d’un intervalle décentré

 

On peut alors montrer que le maître d’ouvrage s’expose, dans cette situation, à davantage de risque que le fournisseur. Si on compare les différents coûts dans les scénarios centrés et décentrés pour, u₀ = u_m = 10 % * y₀ :

Tableau 2

Comparaison du gain manqué, du risque d'avoir trop payé et du coût du risque pour les différents acteurs entre la situation centrée et celle où l'engagement est surestimé

(entre parenthèse est affichée la différence relative de coût par rapport à la situation centrée)

 

On se rend alors compte que le fait d’avoir décentré l’intervalle va avoir tendance :

• pour le fournisseur, à grandement augmenter le risque de gain manqué ; cependant cela va diminuer son risque d’avoir trop payé. L’un dans l’autre, son coût du risque diminue de 13 %;
• pour le maître d’ouvrage, à diminuer le gain manqué et augmenter le trop payé ; cela se traduit par une augmentation significative du coût du risque global de 123 %.

Cette situation engendre donc un risque nettement plus important pour le maître d’ouvrage (coût associé au risqué plus que doublé !). Pour le fournisseur, le risque sera légèrement diminué.

Or c’est la situation qui prévaut actuellement dans les CPE en cours. L’entreprise s’engage en effet généralement sur une valeur de simulation augmentée d’un coefficient de sécurité, à notre connaissance déterminée à dire d’expert. Autour de cette valeur, on crée généralement un tunnel de neutralisation (+/- 5 %) au-delà duquel on déclenche pénalité et intéressement. Ce cas génère ainsi une hausse du coût du risque global de manière très dissymétrique, en défaveur du maître d’ouvrage.

Sensibilité des paramètres

Sauf mention contraire, dans les analyses suivantes, les écarts-types sur la prévision de consommation et sur la mesure sont u₀ = u_m = 10 % y₀.

Position de l’engagement

Dans cette analyse, on va observer l’impact de la surestimation/sous-estimation de la valeur de l’engagement sur le coût du risque. Pour cela on va faire varier la valeur de l’engagement y₀’ de 50 % y₀ à 150 % y₀, pour un intervalle de tolérance défini à +/- 15 % de y₀ : [y₀’ - 15 % y₀ ; y₀’ + 15 % y₀]

Graphique 7

Illustration de l’intervalle de tolérance centré sur une valeur y₀’ de 50 % y₀, y₀ et 150 % y₀, et d’une largeur de 15 % y₀.

 

Les résultats obtenus sont les suivants :

Graphique 8

Variation du coût du risque en fonction de la valeur de l'engagement (y₀', exprimé par rapport à y₀), pour un intervalle de largeur 15 % y₀ et u₀ = u_m = 10 %. Avec décomposition du coût total entre « trop payé » et « gain manqué ».

 

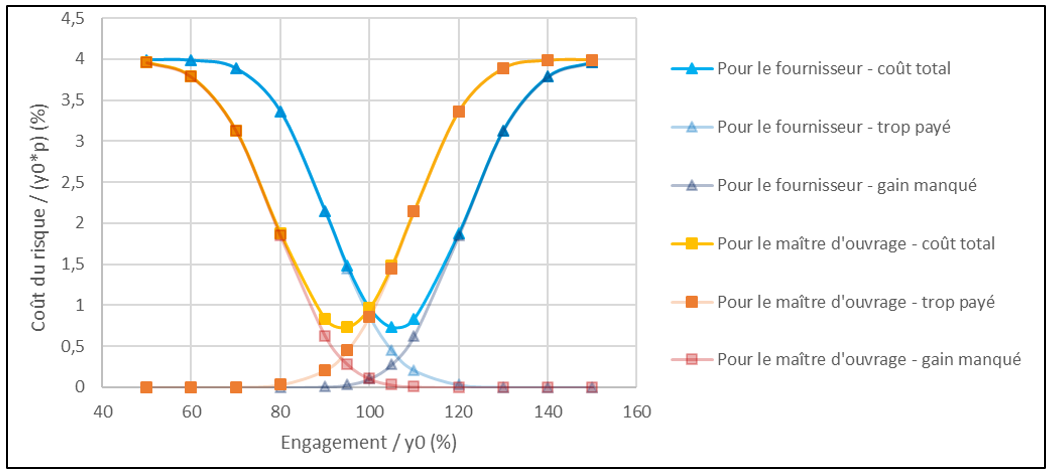
On constate alors que lorsqu’on s’écarte de la valeur y₀, le coût du risque pour chacun des acteurs passe par un minimum. Pour le risque fournisseur, ce minimum est atteint pour une valeur centrale de l’engagement valant environ 105% de y₀. Pour le risque maître d’ouvrage, le minimum est atteint symétriquement pour une valeur d’engagement à environ 95 % de y₀.
Vu le profil des courbes de coût du risque, une valeur centrale d’engagement valant y₀ apparaît comme un bon compromis.

Largeur de l’intervalle de tolérance

Ici, on va analyser l’impact d’un élargissement de l’intervalle de tolérance sur les coûts du risque.

Graphique 9

Illustration des intervalles de tolérance centrés sur y₀, d’une largeur de +/- 5 %, 10 % et 15 %

 

 

Graphique 10

Variation du coût du risque total en fonction de la largeur de l’intervalle de tolérance (tunnel de neutralité) et de u_m, pour un engagement centré sur y₀ et pour u₀ = 10 %

 

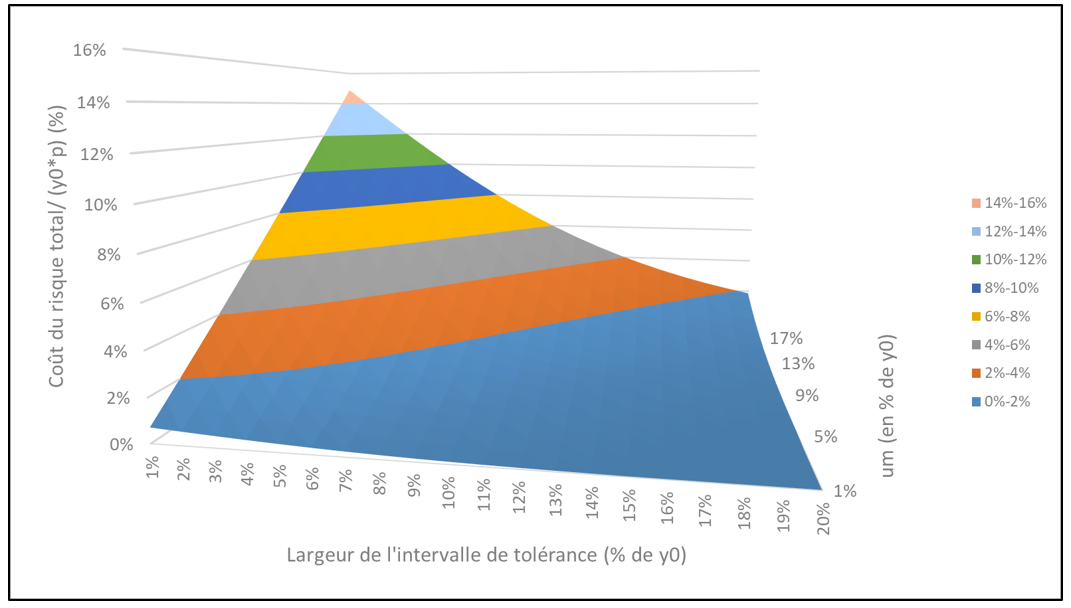
Dans ce cas de figure on observe qu’augmenter la taille de l’intervalle de tolérance fait baisser le coût du risque (de manière similaire pour les deux parties prenantes en y₀’ = y₀ - effet non illustré). Au niveau de y₀’ = y₀ (engagement centré sur y₀) le passage d’un intervalle de tolérance de 5 à 10 % fait diminuer le coût du risque pour chacune des parties prenantes de 57 %, pour u_m = 10 %. L’impact de l’évolution de la largeur de l’intervalle de tolérance augmente avec um, en restant cependant modéré (diminution de 47 % à la place de 57 % lorsque um vaut 15 % à la place de 10 %).

Graphique 11

Variation du coût du risque total en fonction de la largeur de l’intervalle de tolérance (tunnel de neutralité) et de la position de l’engagement par rapport à y₀, pour u_m = u₀ = 10 %

 

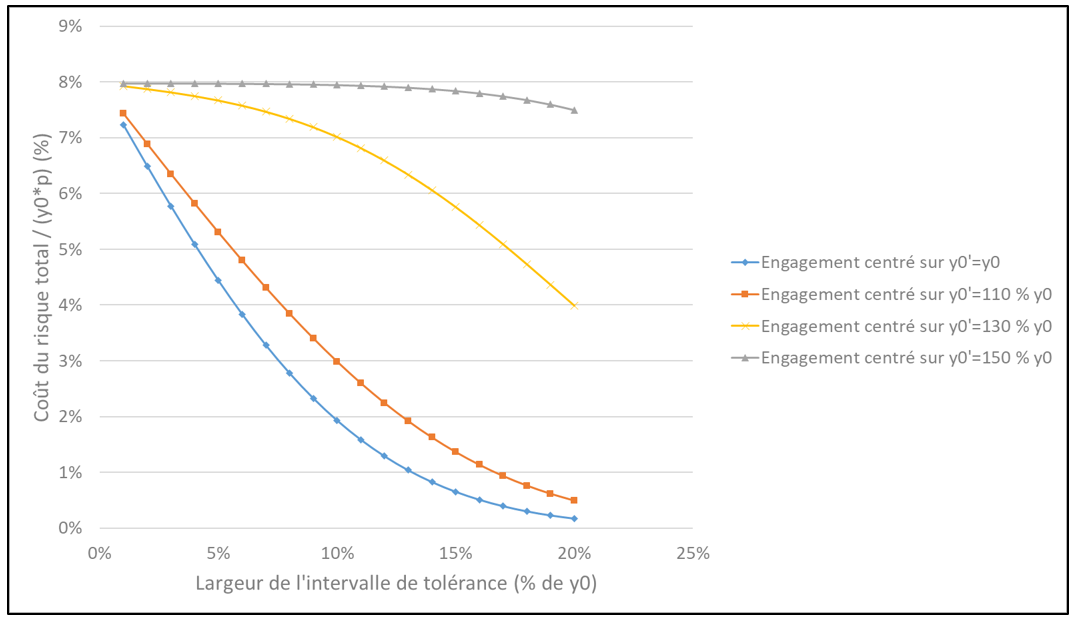
L’influence de la largeur de l’intervalle de tolérance évolue modérement quand um évolue, mais réagit beaucoup plus fortement en fonction de la position de l’engagement. Ainsi la largeur de l’intervalle de tolérance aura un impact très sensible autour de y₀’ = y₀ (engagement centré sur la valeur moyenne prédite par la simulation). Mais lorsque l’on s’éloigne de la valeur y₀, le choix de l’intervalle de tolérance peut devenir quasiment négligeable sur le coût du risque.

Conclusion

Le calcul du coût du risque, présenté en détail dans l’article « Évaluation du coût du risque pour le maître d’ouvrage et le fournisseur de services dans le cadre d’un contrat à garantie de résultats énergétiques », permet une gestion quantitative du risque lié aux incertitudes de mesure et de simulation, dans des opérations avec engagement de résultats.
Elle s’inscrit dans le prolongement d’évolutions récentes dans le domaine, avec notamment :

• La mise à disposition, notamment via l’ouvrage « Méthodes et outils de la garantie de résultats énergétiques, bâtiments tertiaires et collectifs », de méthodes d’analyse d’incertitude dans les outils SED et dans les opérations de mesurage dans le cadre d’engagement de résultats.
• Le développement d’outils de simulation thermique disponibles commercialement permettant de réaliser des propagations d’incertitude (par exemple module AMAPOLA de Pléïades Comfies et Energie+, notamment).

Elle constitue une méthode d’aide à la décision permettant notamment aux acteurs d’opérations avec engagement de résultats de maîtriser :

• Le niveau (coût) des opérations de M&V (Mesure et Vérification) à mettre en œuvre.
• La position de l’engagement par rapport à la valeur moyenne établie par la simulation énergétique dynamique, ainsi que le tunnel de neutralité associé. Il a notamment été montré qu’un engagement positionné autour d’une valeur supérieure à la valeur moyenne obtenue par simulation engendre un transfert de risque très marqué depuis le fournisseur vers le maître d’ouvrage. Or c’est la situation qui prévaut actuellement dans les CPE existant.

Dans le prolongement de ces travaux, il sera intéressant d’affiner la méthodologie à déployer lors de la passation d’un contrat de performance énergétique pour profiter pleinement de ces nouveaux outils.

---

(*) Paul Calberg Ellen est directeur adjoint de Biomasse Normadie. Cet article est une synthèse d'un rapport plus exhaustif préparé dans le cadre des travaux de la Fondation Bâtiment Énergie.